Topic 3: Logarithms & Exercise

LOGARITHMS

Definition of Logarithms

Logarithms are the "opposite" of  exponential just as subtraction is the opposite if addition and division is the opposite of multiplication. Logs "undo" exponential. Technically speaking, log are the inverses of exponential.

In mathematics, the logarithms is the operation to exponential. That's mean the logarithms of a number is the exponent to which another fixed number, the base must be raised to product that number. In simple cases the logarithms of 1000 is 3, as 10 to the power 3 is 1000 (1000 = 10 x 10 x 10 = 10 base of 3).

When asked to solved a logarithmic equation such as Log2 (5x + 7) = 5 or log3 (7x + 3 ) = log3 (5x + 9). The first things we need ti decide is how to solve the logarithms while others are solved by rewriting the logarithms problem in exponential form. How do we decide what is the correct way to solve a logarithm problem? The key is to look at the problem and decide if the problem contains only logarithms or if the problem has terms without logarithms. So the correct way how to solve these type of logarithmic problems is to simply drop the logarithms.

Formula and laws of Logarithms

• Product rule : log_bAC = log_bA + log_bC
• Quotient rule:  log_b(A/C) = log_bA − log_bC
• Power rule:  log_bA^C = C(log_bA)

Basic example of log is:

The logarithm of x to base b, denoted log b (x), is the unique real number y such b^y = x.

Equivalent

Example 1:

How many 2s do we multiply to get 8?

Solution: Answer: 2 × 2 × 2 = 8, so we had to multiply 3 of the 2s to get 8

So the logarithm is 3

Example 2: 
What is log₅(625) ... ?

We are asking "how many 5s need to be multiplied together to get 625?"


Solution: 5 × 5 × 5 × 5 = 625, so we need 4 of the 5s
Answer: log₅(625) = 4

Example 3:

What is log2 (64)??

We are asking "how many 2s need to be multiplied together to get 64"?

Solution:

2 x 2 x 2 x 2 x 2 x 2 = 64, so we need 6 of the 2s

Log 2 (64) = 6

Exponents 

Exponents and Logarithms are related, let's find out how ...

The exponent says how many times to use the number in a multiplication. In this example: 23 = 2 × 2 × 2 = 8 (2 is used 3 times in a multiplication to get 8)

So a logarithm answers a question like this:

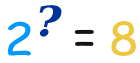
In this way:

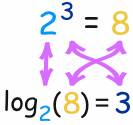
The logarithm tells us what the exponent is!

In that example the "base" is 2 and the "exponent" is 3:

So the logarithm answers the question:

What exponent do we need
(for one number to become another number) ?

The general case is:

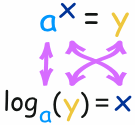
Example 1:

What is log10 (100)?

Solution:

so an exponent of 2 is needed to make 10 into 100. 

so, the answer is log 10 (100) = 2

Example 2:
What is log3 (81)??

Solution:
3x = 81
3 ^ 4 = 81

So an exponent of 4 is needed to make 3 into 81. So the answer is log3 (81) = 4 

Example 3:
What is log6 (36)??

Solution:

6 ^ 2 = 36

So an exponent of 2 is needed to make 6 into 36, the answer is log6 36 = 2

^{OR 👇}

  (Logarithm form)

Example	Become
1)   16 = 24	1)   Log2 16 = 4
2)   64 = 82	2)   Log8 64 = 2

  (Exponent form)

Example	Become
1)   Log 3 27 = 3	1)   27 = 33
2)   Log9 81 = 2	2)   81 = 92

Here some video for you to understand. lets learn from the basic.

 Exercise

...NOW SOLVE THIS...

Convert the following into equivalent form

1) 16 = 2^4

2) 64 = 8^2

3) 49 = 7^2 

 

Convert the following into exponent form

1) Write in exponential form:   log₂32 = 5.

2) Write in logarithmic form:  4⁻²  =1 / 16

   3) Write the exponential form: Log4 16 = 2